Orbit of the Moon

Not to be confused with Lunar orbit in the sense of a selenocentric orbit, that is, an orbit around the Moon

The orbit of the Moon around the Earth is completed in approximately 27.3 days. The Earth and Moon orbit about their common center of mass, which lies about 4,700 kilometres from Earth's center (about three quarters of the Earth's radius). On average, the Moon is at a distance of about 385,000 km from the center of the Earth, which corresponds to about 60 Earth radii. With a mean orbital velocity of 1.023 km/s, the Moon moves relative to the stars each hour by an amount roughly equal to its angular diameter, or by about 0.5°. The Moon differs from most satellites of other planets in that its orbit is close to the plane of the ecliptic, and not to the Earth's equatorial plane. The lunar orbit plane is inclined to the ecliptic by 5.1°, whereas the Moon's spin axis is inclined by only 1.5°.

Properties

The orbit of the Moon is distinctly elliptical with an average eccentricity of 0.0549. The non-circular form of the lunar orbit causes variations in the Moon's angular speed and apparent size as it moves towards and away from an observer on Earth. The mean angular daily movement relative to an imaginary observer at the barycenter is 13.176358° to the east. The orientation of the orbit is not fixed in space, but precesses over time.

Lunar perigee–apogee size comparison

Elongation

Definition of orbital parameters.

The Moon's elongation is its angular distance east of the Sun at any time. At new moon it is zero and the Moon is said to be in conjunction. At full moon the elongation is 180° and it is said to be in opposition. In both cases the moon is in syzygy, that is, the Sun, Moon and Earth are nearly aligned. When elongation is either 90° or 270° the Moon is said to be in quadrature.

Nodes

The nodes are points at which the Moon's orbit crosses the ecliptic. The line of nodes is the intersection between the two respective planes. It has a retrograde motion: for an observer on Earth it rotates westward along the ecliptic with a period of 18.6 years, or 19°21′ per year. When viewed from celestial north, the nodes move clockwise around the Earth, opposite the Earth's own spin and its rotation around the Sun. The Moon crosses the same node every 27.2122 days, an interval called the draconitic month. Lunar and solar eclipses can only occur when the line of nodes points toward the Sun, roughly every 5.4 months. The type of the eclipse depends on Moon's orbital position in that time window.

Line of apsides

Perigee is the distance of closest approach, whereas apogee is its farthest recession. The line joining these two points (the line of apsides) has a progressive motion or advances, that is, it slowly rotates counterclockwise in space in the plane of the Moon's orbit, that is, direct motion, making one complete revolution in 3232.575 days or about 8.85 years.

Lunar standstill

When the ascending node of the moon's orbit coincides with the vernal equinox in the northern hemisphere, the declination of the moon in the sky reaches a maximum at 23°29′ + 5°9′ or 28°36′. This is called the major standstill. Nine and a half years later, when the descending node has come to the same point, the angle is only 23°28′ − 5°8′ or 18°19′, and the declination of the moon is a minimum. This is the minor standstill.

Inclination

Earth's lunar orbit perturbation basics

The mean inclination of the lunar orbit to the ecliptic plane is 5.145°. The rotation axis of the Moon is also not perpendicular to its orbital plane, so the lunar equator is not in the plane of its orbit, but is inclined to it by a constant value of 6.688° (this is the obliquity). One might be tempted to think that as a result of the precession of the Moon's orbital plane, the angle between the lunar equator and the ecliptic would vary between the sum (11.833°) and difference (1.543°) of these two angles. However, as was discovered by Jacques Cassini in 1721, the rotation axis of the Moon precesses with the same rate as its orbital plane, but is 180° out of phase (see Cassini's Laws). Thus, although the rotation axis of the Moon is not fixed with respect to the stars, the angle between the ecliptic and the lunar equator is always 1.543°.

Based on the informal definition that a double planet system must have its barycentre exterior to both bodies, the Earth and Moon are regarded as an ordinary planet–moon system. However, because of the relatively large size of the Moon and the small Earth–Moon mass ratio of about 81:1 when compared to other natural satellites in the Solar System, some consider the Earth–Moon system to be a double planet.

The properties of the orbit described in this section are approximations. The Moon's orbit around the Earth has many irregularities (perturbations), and their study (lunar theory) has occupied astronomers over a long history.^[2]

The Moon orbiting Earth with sizes and distances to scale. Each pixel represents 500 km.

History of observations and measurements

About 3000 years ago, the Babylonians were the first human civilization to keep a consistent record of lunar observations. Clay tablets from that time period found over the territory of present-day Iraq are inscribed with cuneiform recording the times and dates of moonrises and moonsets, the stars that the Moon passed close by, and the time differences between rising and setting of both the Sun and the Moon around the time of the full moon. The Babylonians discovered the three main periods of the Moon's motion and used data analysis to build lunar calendars that extended well into the future.^[2] This use of detailed, systematic observations to make predictions based on experimental data may be classified as the first scientific study in human history. However, Babylonians seem to have lacked any geometrical or physical interpretation of their data, and they could not predict future lunar eclipses (although "warnings" were issued before likely eclipse times).

Ancient Greek astronomers were the first to introduce and analyze mathematical models of the motion of objects in the sky. Ptolemy described lunar motion by using a well-defined geometric model of epicycles and evection.^[2]

Newton was the first to develop a complete theory of motion, mechanics. The sheer wealth of humanity's observations of the lunar motion was the main testbed of his theory.^[2]

Lunar month

There are several ways to consider how much time it takes the Moon to complete one orbit. The sidereal month is the time it takes to make one complete orbit with respect to the fixed stars, which is about 27.3 days. In contrast, the synodic month is the time it takes the Moon to reach the same phase, which takes about 29.5 days. The synodic period is longer than the sidereal period because the Earth–Moon system moves a finite distance in its orbit around the Sun during each sidereal month, and a longer time is required to achieve the same relative geometry. Other definitions for the duration of a lunar month include the time it takes to go from perigee to perigee (the anomalistic month), from ascending node to ascending node (the draconic month), and from two successive passes of the same ecliptic longitude (the tropical month). As a result of the slow precession of the lunar orbit, these latter three periods are only slightly different than the sidereal month. The average length of a calendric month (1/12 of a year) is about 30.4 days.

Tidal evolution

The gravitational attraction that the Moon exerts on Earth is the major cause of tides in the sea; the Sun has a lesser tidal influence. If the Earth possessed a global ocean of uniform depth, the Moon would act to deform both the solid earth (by a small amount) and ocean in the shape of an ellipsoid with high points directly beneath the Moon and on the opposite side of the Earth. However, as a result of the irregular coastline and varying ocean depths, this idealization is only partially realized. While the tidal flow period is generally synchronized to the Moon's orbit around Earth, its phase can vary. In some places on Earth there is only one high tide per day, though this is somewhat rare.

The tidal bulges on Earth are carried ahead of the Earth–Moon axis by a small amount as a result of the Earth's rotation. This is a direct consequence of friction and the dissipation of energy as water moves over the ocean bottom and into or out of bays and estuaries. Each bulge exerts a small amount of gravitational attraction on the Moon, with the bulge closest to the Moon pulling in a direction slightly forward along the Moon's orbit, because the Earth's rotation has carried the bulge forward. The opposing bulge has the opposite effect, but the closer bulge dominates due to its comparative closer distance to the Moon. As a result, some of the Earth's rotational momentum is gradually being transferred to the Moon's orbital momentum, and this causes the Moon to slowly recede from Earth at the rate of approximately 38 millimetres per year. In keeping with the conservation of angular momentum, the Earth's rotation is gradually slowing, and the Earth's day thus lengthens by about 17 microseconds every year. (This would make each Earth day one second longer every 60,000 years or so, and one minute longer every four million years). Looking back, the day was 15 minutes shorter when the dinosaurs roamed the Earth 65 million years ago.) See tidal acceleration for a more detailed description and references.

The Moon is gradually receding from the Earth into a higher orbit, and calculations^[3][4] suggest that this would continue for about fifty billion years. By that time, the Earth and Moon would become caught up in what is called a "spin–orbit resonance" in which the Moon will circle the Earth in about 47 days (currently 29 days), and both Moon and Earth would rotate around their axes in the same time, always facing each other with the same side. However, the slowdown of the Earth's rotation is not occurring fast enough for the rotation to lengthen to a month before other effects change the situation: about 2.1 billion years from now, the increase of the Sun's radiation will have caused the Earth's oceans to vaporize, removing the bulk of the tidal friction and acceleration.

Libration

Animation of the Moon as it cycles through its phases. The apparent wobbling of the Moon is known as libration.

The Moon is in synchronous rotation, meaning that it keeps the same face turned toward the Earth at all times. This synchronous rotation is only true on average because the Moon's orbit has a definite eccentricity. As a result, the angular velocity of the Moon varies as it moves around the Earth, and is hence not always equal to the Moon's rotational velocity. When the Moon is at its perigee, its rotation is slower than its orbital motion, and this allows us to see up to eight degrees of longitude of its eastern (right) far side. Conversely, when the Moon reaches its apogee, its rotation is faster than its orbital motion and this reveals eight degrees of longitude of its western (left) far side. This is referred to as longitudinal libration.

Because the lunar orbit is also inclined to the Earth's ecliptic plane by 5.1°, the rotation axis of the Moon seems to rotate towards and away from us during one complete orbit. This is referred to as latitudinal libration, which allows one to see almost 7° of latitude beyond the pole on the far side. Finally, because the Moon is only about 60 Earth radii away from the Earth's center of mass, an observer at the equator who observes the Moon throughout the night moves laterally by one Earth diameter. This gives rise to a diurnal libration, which allows one to view an additional one degree's worth of lunar longitude. For the same reason, observers at both geographical poles of the Earth would be able to see one additional degree's worth of libration in latitude.

Path of Earth and Moon around Sun

The Moon's orbital path around the Sun (accompanying the Earth in its own path around the Sun) is always convex outwards.^[5] (In this diagram, the Sun is below and to the left of the frame.)

In representations of the solar system, it is common to draw the trajectory of the Earth from the point of view of the Sun, and the trajectory of the Moon from the point of view of the Earth. This could give the impression that the Moon circles around the Earth in such a way that sometimes it goes backwards when viewed from the Sun's perspective. Since the orbital velocity of the Moon about the Earth (1 km/s) is small compared to the orbital velocity of the Earth about the Sun (30 km/s), this never occurs.

Considering the Earth-Moon system as a binary planet, their mutual center of gravity is within the Earth, about 4624 km from its center or 72.6% of its radius. This center of gravity remains in line towards the Moon as the Earth completes its diurnal rotation. It is this mutual center of gravity which defines the path of the Earth-Moon system in solar orbit. Consequently the Earth's center veers inside and outside the orbital path during each synodic month as the Moon moves in the opposite direction.

Unlike most other moons in the solar system, the trajectory of the Moon is very similar to that of the Earth. The Sun's gravitational pull on the Moon is over twice as great as the Earth's pull on the Moon; consequently^[6] the Moon's trajectory is always convex (as seen when looking inward at the entire Moon/Earth/Sun system from a great distance off), and is nowhere concave (from the perspective just mentioned) or looped.^[5][6][7] Although if the gravitational attraction of our Sun could be "turned off", the Moon would continue to make one orbit about the Earth with its current sidereal period.

See also

• Ernest William Brown
• Orbital elements
• Lunar Laser Ranging Experiment
• List of orbits
• Milankovitch cycles

References

The Moon Physical features Internal structure · Gravity field · Topography · Magnetic field · Atmosphere  · Ion tail Orbit Orbit of the Moon · Phases · Solar eclipse · Lunar eclipse · Tides Lunar surface Selenography · Near side · Far side · Lunar mare · Craters · South Pole-Aitken basin · Shackleton crater · Water · Soil · Peak of eternal light · Space weathering · Transient lunar phenomenon Lunar science Geology (timescale) · Giant impact hypothesis · Moon rocks · Lunar meteorites · KREEP · ALSEP · Lunar laser ranging · Late Heavy Bombardment Exploration Exploration of the Moon · Apollo program · Robotic exploration · Future missions · Lunar colonization · Moon Landing hoax accusations Other topics Calendar · Month · The Moon in art and literature · The Moon in mythology · Moon illusion · Lunar effect · Craters named after people · Man in the Moon See also Solar System · Natural satellite

Orbits   Types General Box · Capture · Circular · Elliptical / Highly elliptical · Escape · Graveyard · Hyperbolic trajectory · Inclined / Non-inclined · Osculating · Parabolic trajectory · Parking · Synchronous (semi · sub) Geocentric Geosynchronous · Geostationary · Sun-synchronous · Low Earth · Medium Earth · High Earth · Molniya · Near-equatorial · Orbit of the Moon · Polar · Tundra · Two-line elements About other points Areosynchronous · Areostationary · Halo · Lissajous · Lunar · Heliocentric · Heliosynchronous   Parameters Classical  Inclination ·  Longitude of the ascending node ·  Eccentricity ·  Argument of periapsis ·  Semi-major axis ·  Mean anomaly at epoch Other  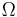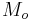True anomaly ·  Semi-minor axis ·  Linear eccentricity ·  Eccentric anomaly ·  Mean longitude ·  True longitude ·  Orbital period   Maneuvers Bi-elliptic transfer · Delta-v budget · Geostationary transfer · Gravity assist · Gravity turn · Hohmann transfer · Low energy transfer · Oberth effect  · Inclination change · Phasing · Rendezvous · Transposition, docking, and extraction · Collision avoidance (spacecraft)   Other orbital mechanics topics Apsis · Celestial coordinate system · Direct motion · Epoch · Ephemeris · Equatorial coordinate system · Ground track · Interplanetary Transport Network · Kepler's laws of planetary motion · Lagrangian point · n-body problem · Orbit equation · Orbital speed · Orbital state vectors · Perturbation · Retrograde motion · Specific orbital energy · Specific relative angular momentum List of orbits